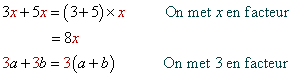Première application : développement

Pour multiplier une somme par un nombre, on peut multiplier chaque terme de la somme par ce nombre.

C'est cette propriété que l'on utilise pour multiplier des nombres de plus de 1 chiffre, par exemple dans la multiplication posée.

Exemple ( calcul numérique ) :
pour calculer 12 fois 53, on ajoute 10 fois 53 et 2 fois 53.

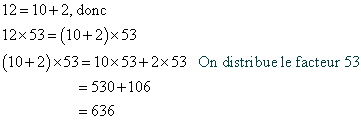
Deuxième application : factorisation

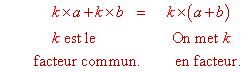
Cette propriété permet de simplifier le calcul de sommes dans lesquelles il y a un facteur commun.

Exemple ( calcul numérique ) :

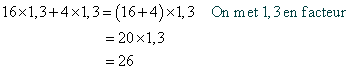
Cette propriété permet de transformer des écritures littérales dans lesquelles on ne peut rien calculer :

Exemple ( calcul littéral ) :

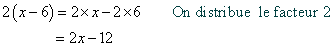
Cette propriété permet de simplifier ou de transformer certaines écritures littérales

Exemple ( calcul littéral ) :