Définition :

Un parallélogramme est un quadrilatère dont les côtés sont parallèles deux à deux.

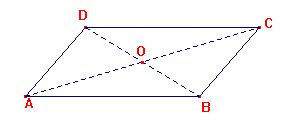
(AB)//(CD) et (AD)//(BC),
donc ABCD est un parallélogramme

image mobile

Propriétes :

ABCD est un parallélogramme, donc (AB)//(CD) et (AD)//(BC).

ABCD est un parallélogramme, donc AB = DC et AD = BC.

- dans un parallélogramme, les côtés opposés sont égaux deux à deux.

ABCD est un parallélogramme dont les diagonales se coupent au point O, donc O est le centre de symétrie de ABCD.

- dans un parallélogramme, le point d'intersection des diagonales est le centre de symétrie. On l'appelle le centre du parallélogramme

ABCD est un parallélogramme dont les diagonales se coupent au point O, donc O est le milieu de [AC] et de [BD].

- dans un parallélogramme, les diagonales se coupent en leur milieu

ABCD est un parallélogramme, donc

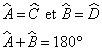
- dans un parallélogramme, les angles opposés sont égaux, et les angles consécutifs sont supplémentaires.