On sait que :
- O est le centre du cercle
- [AB] est un diamètre du cercle
- M est un point du cercle.

On veut prouver que le triangle ABM est rectangle en M.

A. Première démonstration : calcul de la mesure de .

1. Que peut on dire des triangles OAM et OBM ?

A, B et M sont des points du cercle de centre O, donc OA = OM et OM = OB.
Donc OAM et OBM sont deux triangles isocèles en O.

2. On pose = x. Calculer en fonction de x.

OAM est un triangle isocèle en O, or les deux angles à la base d'un triangle isocèle sont égaux, donc =.
La somme des mesures des angles d'un triangle est 180°, donc
=180°-(+)
=180°-2x

3. Calculer , puis , en fonction de x .

A,O et B sont alignés, donc =180°-
=180°-(180°-2x)
=180°-180°+2x
= 2x

OMB est isocèle en O, donc

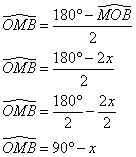
4. En déduire . Conclure.

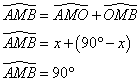
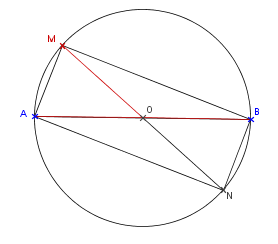
1. Construire le point N, symétrique de M par rapport à O.

N est le symétrique de M par rapport à O, donc O est le milieu de [MN] .
De plus M appartient au cercle de centre O, donc [MN] est un diamètre du cercle.

2. Quelle est la nature de AMBN ?

O est le milieu de [AB] et de [MN], donc les diagonales de AMBN se coupent en leur milieu et sont égales, donc AMBN est un rectangle.

3. Que peut on en déduire ?

Un rectangle a quatre angles droits, donc est droit.