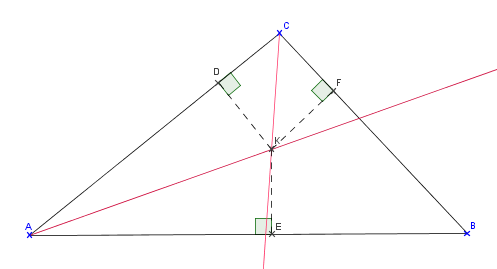
Montrer que les bisectrices des trois angles d'un triangle sont concourantes et que leur point d'intersection est le centre du cercle inscrit dans le triangle.
Sur la figure sont tracées deux bissectrices, leur point d'intersection K et KD, KF et KE sont les distances de K aux droites (AC), (BC) et (AB).
K appartient à la bissectrice de ![]() , donc K est à égale distance de [AC) et [AB), donc KE = KD.
, donc K est à égale distance de [AC) et [AB), donc KE = KD.
K appartient à la bissectrice de ![]() , donc K est à égale distance de [CA) et [CB), donc KD = KF.
, donc K est à égale distance de [CA) et [CB), donc KD = KF.
KE = KD et KD = KF, donc KF = KE.
Tout point situé à égale distance des deux côtés de l'angle appartient à la bissectrice de cet angle, donc K est un point de la bissectrice de ![]() . Les trois bissectrices du triangle passent par K. Elles sont concourantes en K.
. Les trois bissectrices du triangle passent par K. Elles sont concourantes en K.
KE = KD = KF, donc le cercle de centre K qui passe par D passe aussi par E et par F.
![]() , donc (AC) est la tangente au cercle en D.
, donc (AC) est la tangente au cercle en D.
De façon analogue, (BC) et (AB) sont tangentes à ce cercle.
Ce cercle est donc le cercle inscrit dansle triangle.