Equation du premier degré à une inconnue

Vocabulaire :

2 = 1 + 1 est une égalité vraie

2 = 1 + 3 est un égalité fausse (il vaut mieux éviter d'écrire des égalités fausses)

2 = x+ 1 est une égalité qui peut être vraie ou fausse suivant la valeur donnée à x . Cela s'appelle une équation.
Résoudre une équation, c'est trouver la ou les valeurs de x pour lesquelles l'égalité est vraie. Ces valeurs s'appellent les solutions de l'équation.

x , que l'on peut remplacer par n'importe quel nombre, s'appelle une inconnue . Quand cette inconnue n'est ni au carré ni au cube, on dit qu'il s'agit d'une équation du premier degré .

Tester une égalité

L'égalité 4x -5 = 1+ 2x est elle vraie pour x = 2 ?

Calcul du premier membre :

4 2-5 = 8-5
= 3

Calcul du deuxième membre :

1 + 2 2 = 1 + 4
= 5

3 n'est pas égal à 5, donc l'égalité est fausse pour x = 2.

2 n'est pas solution de l'équation 4x -5 = 1+ 2x

Propriétés de l'égalité permettant de résoudre des équations :

Egalité et addition :

Egalité et multiplication :

Si l'égalité a = b est vraie, alors l'égalité a + c = b + c est vraie.

On peut ajouter ( ou soustraire ) un même nombre aux deux membres d'une égalité.

Si l'égalité a = b est vraie et si c est différent de 0,
alors l'égalité a c = b c est vraie.

On peut multiplier (ou diviser) les deux membres d'une égalité par un même nombre différent de 0.

Pourquoi prendre des précautions avec 0 ?
Par exemple 2 = 3 est faux, mais 2 0 = 3 0 est vrai.
Multiplier par 0 peut rendre vraie une égalité qui était fausse. Plutôt gênant...

Technique de résolution d'une équation du premier degré à une inconnue :

Résoudre l'équation :

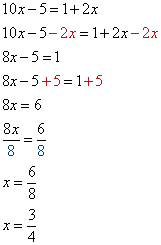
La solution de l'équation est .

Remarque :
est une équation que l'on peut résoudre en " remontant" le programme de calcul associé :
On choisit une nombre
On le multiplie par 8
On soustrait 5
On obtient 1
En remontnant le programme de calcul :
On choisit le nombre1
On ajoute 5, ce qui donne 6, puis on divise par 8, ce qui donne c'est à dire .

On soustrait 2x aux deux membres de l'égalité pour rassembler les termes en x dans un seul des deux membres.
Puis on compte.
On ajoute 5 aux deux membres de l'égalité pour isoler les termes en x .
Puis on compte.
On divise les deux membres de l'égalité par 8 pour isoler le x .
Et on trouve x = . Pour que 4 x -5 soit égal à 1+2 x , il faut que x soit égal à .
C'est la seule solution.

Une équation du premier degré à une inconnue a, en général, une seule solution.

Equation qui n'a pas de solution :

3( 1-2 x ) = 2 - 6 x
3 - 6 x = 2 - 6 x
3 - 6 x+6x = 2 - 6 x +6x
3 = 2

3 = 2 est une égalité fausse, donc l'égalité de départ est fausse, quelle que soit la valeur donnée à x .
Cette équation n'a pas de solution.

Equation qui a une infinité de solutions :

3( 1-2 x ) = 3 - 6 x
3 - 6 x = 3 - 6 x
3 - 6x+6x = 3 - 6 x +6x
3 = 3

3 = 3 est une égalité vraie, donc l'égalité de départ est vraie, quelle que soit la valeur donnée à x .
Tous les nombres sont solutions de cette équation..