A.

SAB est un cône de hauteur OS = 10 cm et dont le rayon de la base est 3 cm.
1. Calculer SA. En donner la valeur arrondie au mm.

OS est la hauteur du cône, donc le triangle OSA est rectangle en O.
Dans le triangle OSA rectangle en O, j'utilise le théorème de Pythagore.

2. Calculer la valeur arrondie au degré de .
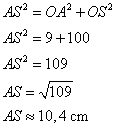
Dans le triangle AOS rectangle en O,

3. Construire le patron de ce cône.
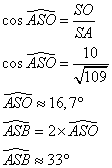
Il faut calculer l'angle au centre du secteur circulaire.


La longueur du secteur circulaire est 6
Le rayon du cercle est AS.
La longueur du cercle, correspondant à un angle au centre de 360°, est

longueur	x	6
angle	360

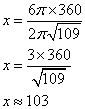
L'angle au centre du secteur circulaire est 103°.

4. Calculer le volume de ce cône. En donner la valeur arrondie au mm³

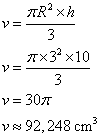
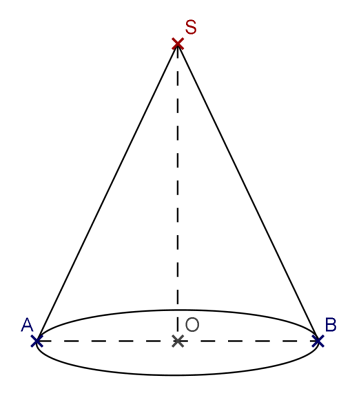
Patron du cône :

B.

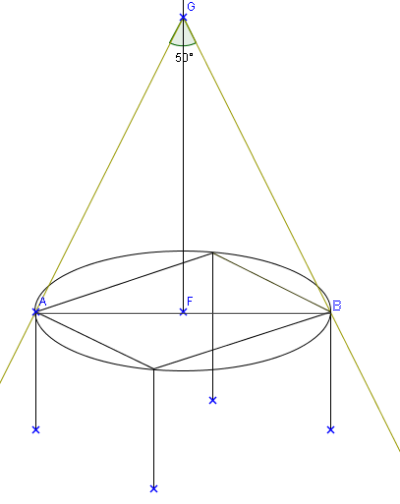
Un spot envoie un cône de lumière au dessus d'une table carrée de côté 1,20 m avec un angle de 50°.
On souhaite que la table soit entièrement éclairée.
A quelle hauteur au minimum faut il suspendre le spot lumineux ?

Il faut calculer GF.
Le triangle AGF est rectangle en F.
L'angle mesure la moitié de l'angle, c'est à dire 25 °.
Les deux angles aigus d'un triangle rectangle sont complémentaires, donc = 90°-25°
= 65°

Le rayon du cercle est égal à la moitié de la diagonale de la table.
Le dessus de la table est un carré, donc on utilise le théorème de Pythagore

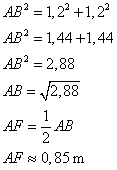
Dans le triangle AGF rectangle en F,


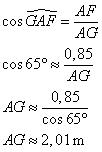
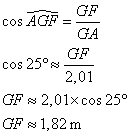
Il faut suspendre la lampe à au moins 1,82 m au dessus de la table

retour