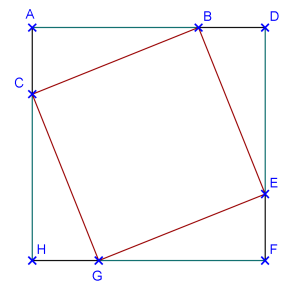
Dans cette figure, AHFD est un carré.
B est le point de [AD] tel que AB = a
E est le point de [DF] tel que DE = a
G est le point de [FH] tel que FG = a
C est le point de [AH] tel que HC = a

1. On pose AC = b
Quels sont les segments de mesure b ?
AC = BD = EF = GH = b

2. On pose BC = c
Quels sont les segments de mesure c ?
Deux triangles rectangles dont les deux côtés de l'angle droit sont égaux sont superposables, donc
BC = BE = GE = GC = c

Que peut-on en déduire pour CBEG ?
Les quatre côtés de CBEG sont éguax, donc CBEG est un losange.

3. Que peut-on dire de et ?

etsont les deux angles aigus d'un triangle rectangle, donc etsont complémentaires ( += 90°)

Que peut on dire de et ?

Deux triangles rectangles dont les deux côtés de l'angle droit sont égaux sont superposables, donc  =,
donc  += 90°

Calculer .

=180° - -
=180° -( +)
= 180° - 90°
= 90°

4. Que peut on en déduire pour CBEG ?
CBEG est un losange qui a un angle droit, donc CBEG est un carré.

5. Calculer AD, puis l'aire de ADFH en fonction de a et b.
En donner la forme développée.
AD = a + b

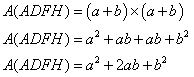
6. En utilisant le découpage de ADFH, calculer l'aire de ADFH en fonction de a, b et c.
L'aire de ADFH est égale à quatre fois l'aire du triangle ABC plus l'aire du carré CBEG.

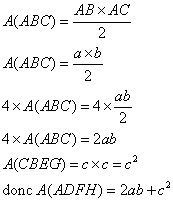
7. Les deux aires sont égales. Que peut on en déduire ?

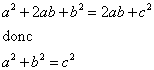
c est la longueur de l'hypoténuse. Donc :

dans un triangle rectangle, le carré de l'hypoténuse est égal à la somme des carrés des deux autres côtés.