Propriétés des diviseurs

Calcul du PGCD de deux nombres : algorithme d'Euclide.
a et b sont deux entiers naturels différents de 0. La division euclidienne de a par b donne a = b q + r q est le quotient entier de a par b et r est le reste.
Si un nombre divise b, alors il divise b q. Si un nombre divise b et b q, alors il divise leur différence a - b q, donc il divise r. Le PGCD de a et b divise donc le plus petit de ces deux nombres et le reste de la division euclidienne de a par b. On calcule donc le reste de la division euclidienne de a par b, puis le reste de la division euclidienne du plus petit de ces deux nombres et du reste, etc. Le dernier reste non nul est le PGCD des deux nombres.
A la main :	Avec un tableur :
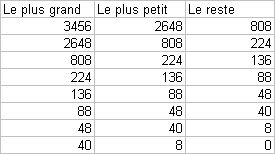
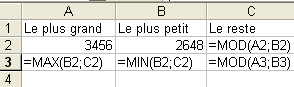
Le PGCD de 3456 et 2648 est 8	MOD(A2,B2) donne le reste de la division euclidienne du contenu de la case A2 par le contenu de la case B2.
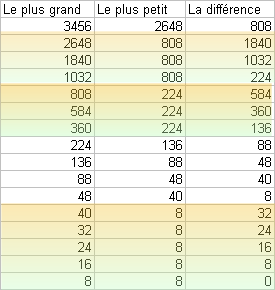
Comparaison des deux méthodes :	Le reste de la division euclidienne de a par b s'obtient sur une calculatrice scientifique avec la touche . On peut l'obtenir en tapant , puis en calculant le reste, en soustrayant à a le produit de b par la partie entière du quotient.
	L'algorithme d'Euclide est plus rapide : certaines divisions remplacent ici 4 ou 5 soustractions successives.