Sur la figure ci contre, le triangle ABC est rectangle et isocèle en A.
On donne BC = 8,4 cm.
Le point M appartient au segment [BC].
Le quadrilatère MNPQ est un rectangle.

1. a ) Donner la valeur de l'angle .
ABC est rectangle en A, donc
Le deux angles à la base d'un triangle isocèle sont égaux, donc

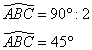
b ) En déduire que BMN et CPQ sont deux triangles rectangles et isocèles.
BMN est un triangle rectangle en M et
BMN a deux angles égaux, donc BMN est isocèle.
La démonstration est analogue pour PQC.

2. On pose BM = 1,5 cm.
Calculer MQ et l'aire du rectangle MNPQ.

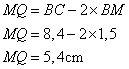
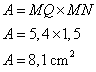
3. On pose BM = x .
a ) Exprimer les dimensions MQ et MN en fonction de x .

b ) En déduire que l'aire du rectangle MNPQ, notée A(x), s'écrit
.

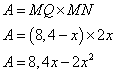
4. a ) Recopier et compléter le tableau suivant à l'aide des questions 2. et 3. b.

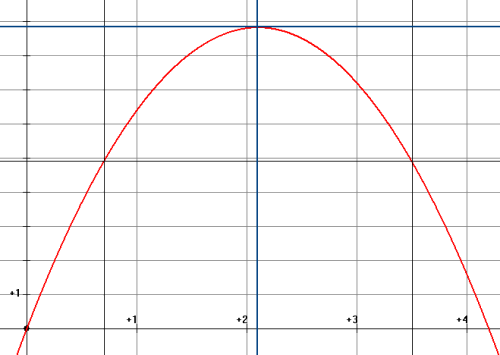
b) Sur le graphique, on a tracé la représentation de l'aire du triangle en fonction de x .
Placer sur ce document les points dont on a obtenu les coordonnées dans la question 4.a.

5. Par lecture graphique, déterminer :
a ) Pour quelles valeurs de x l'aire du rectangle est 4,9
L'aire du rectangle est 4,9 pour
( les traits noirs sur le graphique )
b ) Pour quelle valeur de x l'aire du rectangle est maximale.
L'aire du rectangle est maximale pour ( les droites bleues sur la figure )