 Parallélogrammes
Parallélogrammes 
Définition :
Un parallélogramme est un quadrilatère dont les côtés sont parallèles deux à deux.
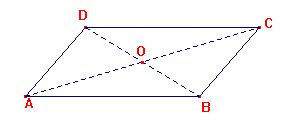
Propriétes :
- dans un parallélogramme, les côtés opposés sont égaux
- dans un parallélogramme, les diagonales se coupent en leur milieu
- dans un parallélogramme, le point d'intersection des diagonales est le centre de symétrie. On l'appelle le centre du parallélogramme
- dans un parallélogramme, les angles opposés sont égaux, et les angles consécutifs sont supplémentaires.
Conditions pour qu'un quadrilatère soit un parallélogramme :
- si un quadrilatère a des côtés opposés égaux deux à deux, alors c'est un parallélogramme.
- si un quadrilatère à deux côtés à la fois parallèles et égaux, alors c'est un parallélogramme.
- si un quadrilatère a un centre de symétrie, alors c'est un parallélogramme.
- si un quadilatère a des diagonales qui se coupent en leur milieu, alors c'est un parallélogramme.
Définition :
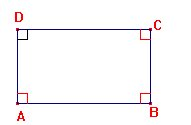
Un rectangle est un quadrilatère qui a trois angles droits ( donc il en a quatre).
Propriétés:
Un rectangle est un parallélogramme. Donc il a toutes les propriétés du parallélogramme.
- les diagonales d'un rectangle sont égales.
- un rectangle a deux axes de symétrie : les médiatrices des côtés.
Conditions pour qu'un parallélogramme soit un rectangle :
- si un parallélogramme a des diagonales égales, alors c'est un rectangle.
- si un parallélogramme a un angle droit, alors c'est un rectangle.
Définition :
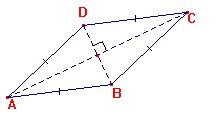
Un losange est un quadrilatère qui a quatre côtés égaux.
Propriétés:
Un losange est un parallélogramme. Donc il a toutes les propriétés du parallélogramme.
de plus:
- les diagonales d'un losange sont perpendiculaires.
- un losange a deux axes de symétrie : les diagonales.
Conditions pour qu'un parallélogramme soit un losange :
- si un parallélogramme a des diagonales perpendiculaires, alors c'est un losange.
- si un parallélogramme a deux côtés consécutifs égaux, alors c'est un losange.
Définition :
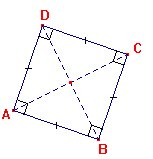
Un carré est un rectangle et un losange.
Un carré a donc toutes les propriétés du parallélogramme, du rectangle et du losange.
Conditions pour qu'un parallélogramme soit un carré :
Toutes les combinaisons sont possibles. Il faut prouver que le quadrilatère est un losange et aussi un rectangle.