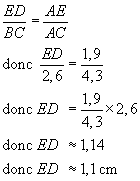Utilisation du théorème de Thalès pour calculer des longueurs - Corrections 
Indiquer la longueur que l'on peut calculer, puis calculer sa valeur arrondie au mm.
A.
On sait que :
(AB)//(DE)
AB = 4,6 cm; BC = 3,5 cm; CD = 1,4 cm
Calcul de DE :
(AB)//(DE), donc j'utilise le théorème de Thalès:
Les deux triangles dont les longueurs sont proportionnelles sont CAB et CED.
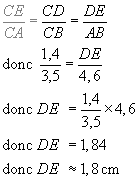
B.
On sait que :
(AB)//(EC)
AD = 3,6 cm; DE = 2,7cm et BD = 6,2 cm.
Calcul de DC :
Les deux triangles dont les longueurs sont proportionnelles sont DAB et DEC.
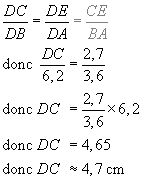
C.
On sait que :
(AE) 
(AC); (DB) (AC)
AE = 3 cm; BD = 2,2 cm et BC = 3,3 cm.
(AE) (AC) et (DB) (AC), donc (AE)//(BD)
Calcul de AC :
(AE)//(BD) , donc j'utilise le théorème de Thalès
Les deux triangles dont les longueurs sont proportionnelles sont CAE et CBD.
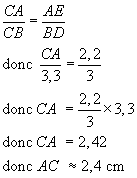
D.
On sait que :
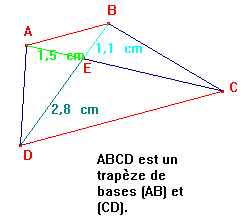
ABCD est un trapèze de bases (AB) et (CD).
AE =1,5 cm; BE = 1,1cm et DE = 2,8 cm.
Calcul de EC :
(AB)//(CD) , donc j'utilise le théorème de Thalès
Les deux triangles dont les longueurs sont proportionnelles sont ECD et EAB.
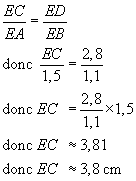
E.
On sait que :
(BC) (BD); (ED) (BD)
BC = 2,6 cm; AC = 4,3 cm et AE = 1,9 cm.
(ED) (BD) et (BC) (BD), donc (BC)//(ED).
Calcul de ED :
(BC)//(ED) , donc j'utilise le théorème de Thalès
Les deux triangles dont les longueurs sont proportionnelles sont AED et ACB.
