A.

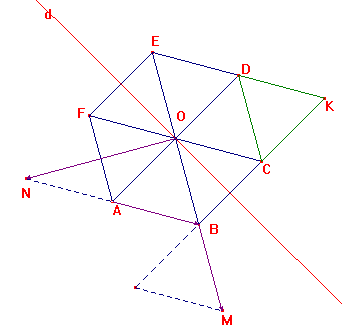
Sur la figure ci-contre, ABCDEF est un hexagone régulier de centre O.
1. Le triangle ABO et le triangle CDO sont symétriques par rapport à la droite d. Construire la droite d.

La droite d est rouge.

2. Quel est le triangle image du triangle ABO dans la translation qui transforme C en D ?
L'image de ABO par la tranlation qui transforme C en D est OEF.

3. Construire l'image du triangle ODE par la translation de vecteur .
C'est le triangle CDK.

4. OAF est l'image de OAB par une transformation du plan. Laquelle ?
OAF est l'image de OAB par la symétrie d'axe (OA) ou par la rotation de centre O, de sens indirect et d'angle 60°.

5. a ) Construire le point M tel que

B.

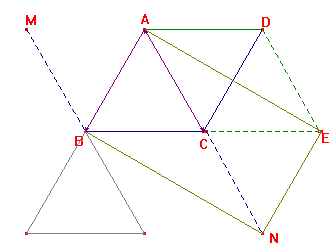
Soit ABC un triangle équilatéral tel que AB = 5cm.
Soit D le point tel que ABCD soit un parallélogramme.
Soit E le symétrique de B par rapport à C.
1. Quel sont les vecteurs égaux à  ? Justifier.
ABCD est un parallélograme, donc .
E est le symétrique de B par rapport à C, donc C est le milieu de [BE], donc
2. Montrer que ADEC est un parallélogramme.
et , donc , donc ADEC est un parallélogramme.
3. Construire le point M tel que .
4. Construire le point N tel que .
5. Que peut on dire de AENB ? Justifier.
, donc C est le milieu de [AN]. De plus , C est le milieu de [BE]. Donc AENB est un parallélogramme.
ABC est un triangle équilatéral, donc AC = BC. Donc BE = AN.
AENB est un parallélogramme dont les diagonales sont égales, c'est à dire un rectangle.
6. Recopier et compléter en utilisant des points déjà tracés :
( relation de Chasles )


7. AMB est l'image de CEN par une translation. Quel est le vecteur de la translation ?

8. Construire l'image de ABC par la translation de vecteur .
On obtient le triangle gris.

C.

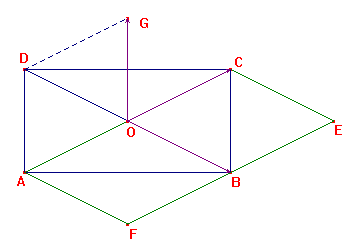
ABCD est un rectangle de centre O tel que AB = 6 cm et AD = 3 cm.
1. a ) Construire le point E tel que .
b ) Construire le point F tel que .
2. a ) Citer tous les vecteurs de la figure égaux à .
Les diagonales d'un rectangle se coupent en leur milieu, donc O est le milieu de [DB], donc .
, donc . De plus, .
b. Que peut on dire de ACEF ? Le démontrer.
et , donc , donc AFEC est un parallélogramme.
3. Le triangle AOD est l'image du triangle CEB par une translation. Quel est le vecteur de la translation ?
AOD est l'image du triangle CEB par la translation de vecteur .
4. Recopier et compléter, en utilisant des points de la figure :



5. Construire le point G tel que .