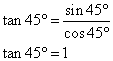Sinus, cosinus et tangente d'un angle de 30° et d'un angle de 60°.

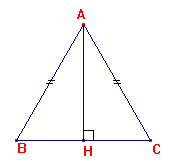
ABC est un triangle équilatéral de côté 1.
[AH ] est  la hauteur issue de A de ABC.
1. Calculer BH, puis AH.
[AH ] est  la hauteur issue de A de ABC, donc [AH] est aussi la médiane de ABC,
donc BH = .
Dans le triangle ABH rectangle en H, j'utilise le théorème de Pythagore

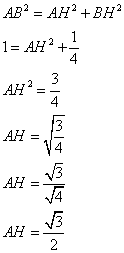
2. Quelle est la mesure de ? En déduire la mesure de .
ABC est un triangle équilatéral, donc =60°
[AH ] est  la hauteur issue de A de ABC, donc [AH] est aussi la bissectrice de , donc
=30°.

3. Calculer le sinus et le cosinus de ces angles.
Dans le triangle ABH rectangle en H,

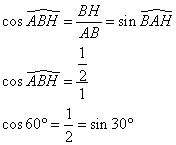
3. suite :

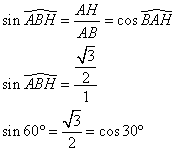
4. En déduire la tangente de ces angles.

Sinus, cosinus et tangente d'un angle de 45°.

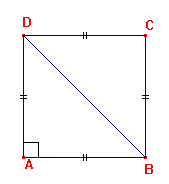
ABCD est un carré de côté 1.
1. Calculer BD.
Dans le triangle ABD rectangle en A, j'utilise le théorème de Pythagore :

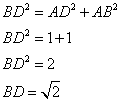
2. Quelle est la mesure de ?
ABD est un triangle rectangle et isocèle, donc = 90° : 2, =45°.

3. Calculer le sinus et le cosinus de cet angle.
Dans le triangle ABD rectangle en A,

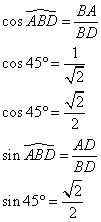
4. En déduire la tangente de cet angle.