A.

La pyramide de Kheops est une pyramide régulière à base carrée.
ABDCF en est une représentation en perspective cavalière.
Le côté du carré mesure environ 230 m et la hauteur de la pyramide est 146 m.

1. Calculer AE, puis AF
ABDC est un carré, donc et ABD est un triangle rectangle en B.
Dans le triangle ABD rectangle en B, j'utilise le théorème de Pythagore.

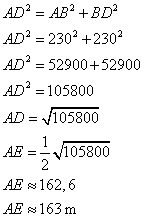
(EF) est la hauteur de la pyramide, donc AEF est un triangle rectangle en E.
Dans le triangle AEF rectangle en E, j'utilise le théorème de Pythagore.

2. Pour en construire une maquette, Mouna choisit de dessiner un carré de 11,5 cm pour représenter la base.

a ) Quelle est l'échelle de la maquette ?
La taille réelle est 230 m , soit 23000 cm.
La taille sur le dessin est 11,5 cm.

La maquette est au e.

b ) Quelle est alors la hauteur de la maquette ?
La hauteur réelle est 146m = 14600 cm.
14600 : 2000 = 7,3
La hauteur de la maquette est 7,3 cm.

c ) Quelle est la mesure de AF sur la maquette ?
219 m = 21900 cm
21900 : 2000 = 10,95
La mesure de AF sur le dessin est 11 cm.

d ) Dessiner la patron de la maquette.

Patron de la maquette :

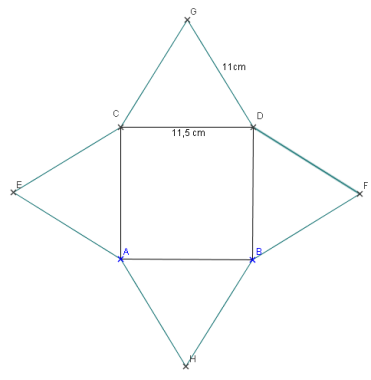
B.

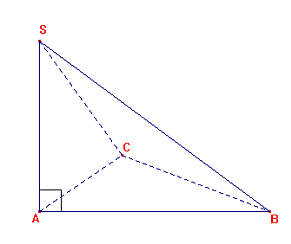
La figure ci-contre est la représentation en perspective cavalière d'une pyramide à base triangulaire.
La base est le triangle ABC, tel que AB = 8 cm, AC = 4,8 cm et BC = 6,4 cm.

La hauteur est [SA], tel que SA= 7 cm.

1. Montrer que la base ABC est un triangle rectangle.

Le côté le plus long est [AB]

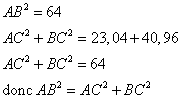
donc ABC est rectangle en C d'après la réciproque du théorème de Pythagore.

2. Calculer SB. En donner la valeur arrondie au mm.
ABC est un triangle rectangle en A, donc j'utilise le théorème de Pythagore

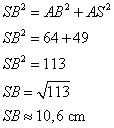
3. Calculer La valeur arrondie au degré de l'angle .
ASB est un triangle rectangle en A

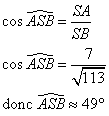
4. Construire un patron de cette pyramide.

retour