A.
ABCDEFGH est un cube d'arête 5 cm.
ABCDE est la pyramide de base ABCD et de hauteur [AE].
1. Indiquer la nature de ABCD, ABE, ADE, DCE et BCE.
ABCDEFGH est un cube, donc ABCD est un carré.
ABFE est un carré, donc ABF est un triangle rectangle et isocèle en A.
ADHE est un carré, donc ADE est un triangle rectangle et isocèle en A.
(CD) est orthogonale au plan de ADHE, donc CDE est un triangle rectangle en D.
(CB) est orthogonale au plan de ADFE, donc BCE est un triangle rectangle en B.
2. Calculer BE, puis CE. En donner la valeur arrondie au mm.
Dans le triangle ABE rectangle en A, j'utilise le théorème de Pythagore.
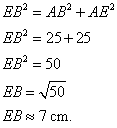
Dans le triangle BCE rectangle en B, j'utilise le théorème de Pythagore
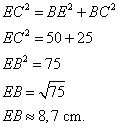
4. Calculer le volume du cube, puis le volume de la pyramide.
![]()
Le volume du cube est 125![]()
Le volume de la pyramide est égal au tiers du volue du cube, c'est à dire environ 42![]() .
.

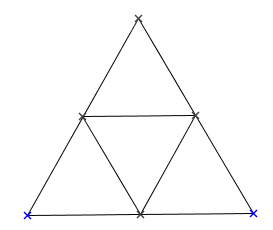
3. Dessiner le patron de la pyramide ABCDE.

B.
On construit une pyramide ACHF dans un cube ABCDEFGH d'arête 10 cm.
1. Décrire cette pyramide.
La pyramide a quatre faces triangulaires. C'est un tétraèdre.
Les arêtes sont toutes des diagonales d'un carré de côté 10 cm. Elles sont toutes égales. La pyramide est donc formée de quatre triangles équilatéraux : c'est un tétraèdre régulier.
2. Calculer la longueur d'une arête.
Calcul de AC :
ABCDEFGH est un cube, donc ABCD est un carré, donc ABC est rectagle en B.
ABC est un triangle rectangle en B, donc j'utilise le théorème de Pythagore.
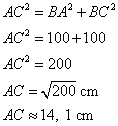
3. Construire le patron de cette pyramide.
Le patron est formé de quatre triangles équilatéraux de côté 14,1 cm.