A.

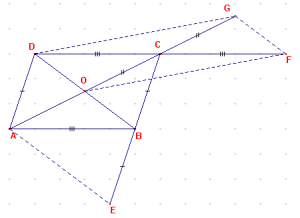
1. Dans le repère (A,B,D), donner les coordonnées de A, B, C et D.
A( 0,0 ) ( A est l'origine du repère )
B ( 1,0 ) ( B indique l'unité sur l'axe des abscisses )
C ( 1,1)
D ( 0,1) ( D indique l'unité sur l'axe des ordonnées )
2. Soit E le symétrique de A par rapport à B
Soit F le symétrique de B par rapport à C
Soient G le symétrique de C par rapport à D et H le symétrique de D par rapport à A.
Donner les coordonnées de ces points dans le repère (A,B,D)
E ( 2;0 ) F (1;2) G ( -1.1) H ( (0;-1)
3. Montrer que EFGH est un parallélogramme.

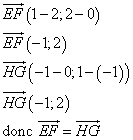
donc EFGH est un parallélogramme.

B.

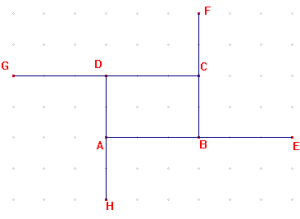
1. ABCD est un parallélogramme de centre O.
Dans le repère ( A, B, D), donner les coordonnées des points A,B,C,D et O
A( 0; 0 ) B( 1; 0 ) C( 1;1 ) D( 0 ; 1 ) O( 0,5 ; 0,5 )
2. Soit E le symétrique de C par rapport à B, F le symétrique de D par rapport à C et G le symétrique de O par rapport à C.
Donner les coordonnées de E, F et G dans le repère ( A,B,D).
E(1; -1 ) F ( 2 ; 1 ) G ( 1,5 ; 1,5 )
3. Que peut on dire de ADBE ? Pourquoi ?

donc ADBE est un parallélogramme.
4. Que peut on dire de ODGF ? Pourquoi ?
F est le symétrique de D par rapport à C et G est le symétrique de O par rapport à C, donc C est le centre de symétrie de OFGD, donc OFGD est un parallélogramme.