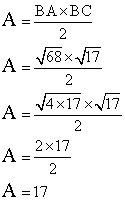Distance dans un repère orthonormal, triangles, parallélogrammes particuliers.
Distance dans un repère orthonormal, triangles, parallélogrammes particuliers. 
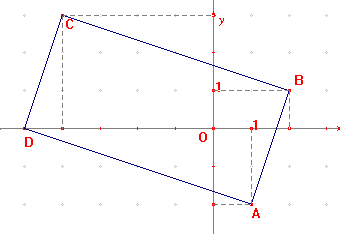
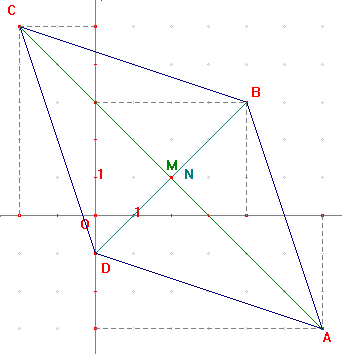
Si l'unité sur les deux axes est le centimère, on peut vérifier les calculs de longueur sur la figure.
A.
A( -1 ; 2) B( 4 ; 3 ) C ( 5 ; -2 )
Montrer que ABC est un triangle rectangle et isocèle
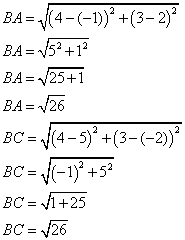
BA = BC, donc ABC est isocèle en B.
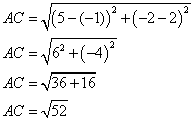
AC est le côté le plus long
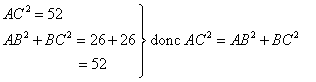
donc ABC est un triangle rectangle en B d'après la réciproque du théorème de Pythagore.

B.
A( 1 ; -2) B( 2 ; 1 ) C ( -4 ; 3 ) D( -5 ; 0 )
1. Calculer les coordonnées de ![]() .
.
Que peut on dire de ABCD
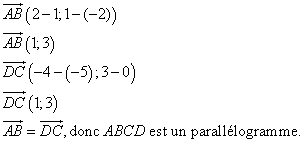
2. Calculer AC et BD.
Que peut on dire de ABCD ?
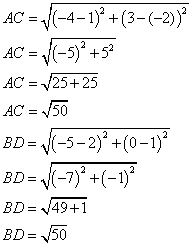
AC = BD, donc ABCD est un parallélogramme dont les diagonales sont égales, c'est à dire un rectangle.
C.
A( 6 ; -3) B( 4 ; 3 ) C ( -2 ; 5 ) D( 0 ; -1 )
1. Calculer les coordonnées du point M, milieu de [AC].
Calculer les coordonnées du point N, milieu de [BD].
Que peut on en déduire pour ABCD ?
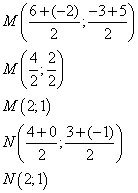
M et N sont confondus, donc les diagonales de ABCD se coupent en leur milieu, donc ABCD est un parallélogramme.
2. Calculer AB et AD.
Que peut on en déduire pour ABCD ?
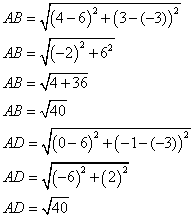
AB=AB, donc ABCD est un parallélogramme qui a deux côtés consécutifs égaux,c 'est à dire un losange.
3. Calculer le périmètre de ABCD.
Un losange a quatre côtés égaux, donc
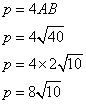
D.
A( -4 ; -1) B( 2 ; 1 ) C ( 0 ; -5 )
1. Montrer que ABC est un triangle isocèle.
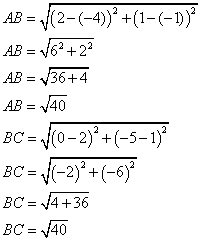
AB=BC, donc ABC est un triangle isocèle en B.
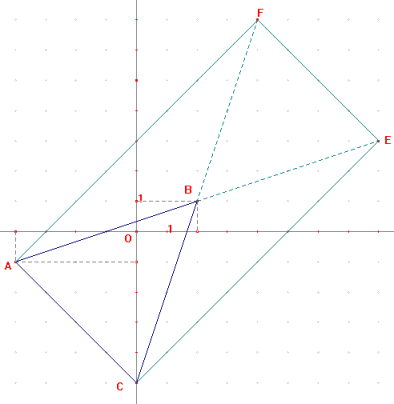
2. Soit E le symétrique de A par rapport à B et F le symétrique de C par rapport à B.
Que peut on dire de ACEF ?
E est le symétrique de A par rapport à B , donc B est le mileu de [AE].
F est le symétrique de C par rapport à B , donc B est le mileu de [CF].
Les diagonales de ACEF se coupent en leur milieu , donc ACEF est un parallélogramme.
AB=BC, donc AE = CF.
Donc ACEF est un parallélogramme dont les diagonales sont égales, c'est à dire un rectangle.
E.
A( -5 ; 0) B( 3 ; 2 ) C ( 4 ; -2 )
1. Montrer que ABC est un triangle rectangle.
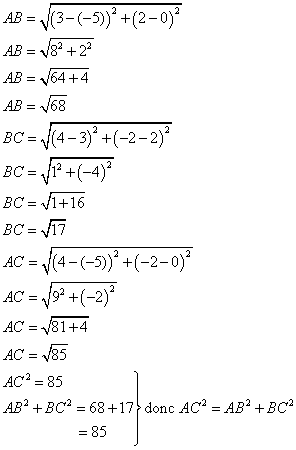
donc ABC est un triangle rectangle en B d'après la réciproque du théorème de Pythagore.
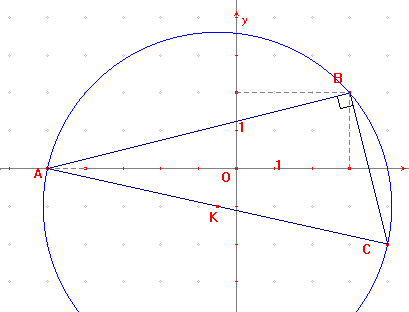
2. Tracer le cercle circonscrit à ce triangle. Soit K son centre.
Préciser la position de K et calculer le rayon du cercle.
Le centre du cercle circonscrit à un triangle rectangle est le milieu de l'hypoténuse, donc le centre du cercle circonscrit à ABC est le milieu de [AC].
le rayon est KA.
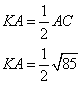
3. Calculer l'aire du triangle ABC.