Coordonnées, distances 
A.
1. Placer les points A (-2 ;5), B ( 3 ;1) et C(-1 ;-4).
2. Calculer la longueur AC. En donner la valeur exacte.
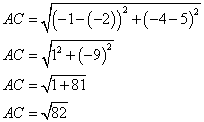
3. Sachant de plus que AB = BC = 
, déterminer la nature du triangle ABC.
Le côté le plus long est [AC].
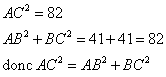
Donc ABC est rectangle en B, d'après la réciproque du théorème de Pythagore.
ABC est rectangle et isocèle en B.
4. Construire le point D pour que le quadrilatère ABCD soit un parallélogramme.
a ) Déterminer les coordonnées de D.
ABCD est un parallélogramme, donc 
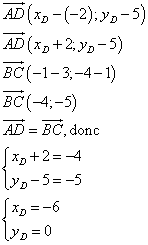
b ) Le quadrilatère ABCD est un parallélogramme particulier. Lequel ? Justifier.
ABCD est un parallélogramme qui a deux côtés consécutifs égaux, donc un losange, et un angle droit, donc un rectangle. Donc ABCD est un carré.
5. Tracer le cercle circonscrit à ABC. Soit K son centre.
a ) Préciser la position du point K.
ABC est un triangle rectangle, donc K est le milieu de l'hypoténuse [BC].
b ) Déterminer les coordonnées du point K.
6. Construire le point M, image de B par la translation de vecteur 
.
a ) Que peut on dire de CDBM ? Justifier.
b ) Que représente B pour [AM ] ? Justifier.
c ) Calculer les coordonnées du vecteur 
.
B.
Dans un repère orthonormal (O, I, J), placer les points suivants :
A ( - 4 , 1 ) B ( 0 , 4 ) C ( 6 , -4 ).
1. a ) Calculer AB, AC et BC.
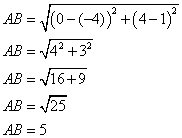
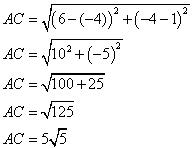
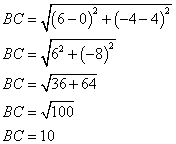
b ) En déduire que ABC est un triangle rectangle.
Le côté le plus long est [AC].
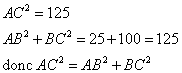
donc ABC est rectangle en B, d'après le réciproque du théorème de Pythagore.
2. Calculer la valeur arrondie au degré de l'angle 
Dans le triangle ABC rectangle en B
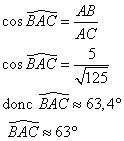
3. Calculer les coordonnées du milieu M de [AC].
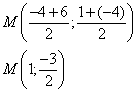
4. a ) Soit D ( 2, -7 ). Monter que D est le symétrique de B par rapport à M.
Soit N le milieu de [BD].
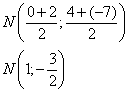
Donc M est le milieu de [BD], donc D est le symétrique de B par rapport à M.
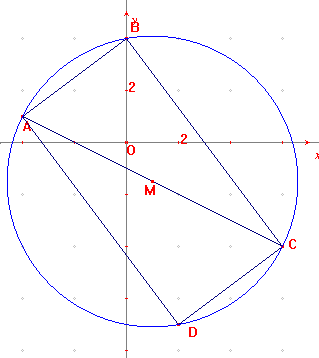
b ) Quelle est la nature de ABCD ? Justifier.
Les diagonales de ABCD se coupent en leur milieu, M, donc ABCD est un parallélogramme. De plus ABCD a un angle droit. Donc ABCD est un rectangle.
5. Tracer le cercle circonscrit au triangle ABC.
a ) Quel est son centre ?
Le centre du cercle circonscrit à ABC est le milieu de l'hypoténuse [AC], c'est à dire M.
b ) Calculer son rayon.
Le rayon est la moitié du diamètre AC
c ) Le cercle passe par D. Pourquoi ?
D est le symétrique de B par rapport à M, donc BM = MD. Le cercle passe par D.