A.

Un père dispose de 1600 € pour ses trois enfants. Il veut que l'aîné ait 200 € de plus que le second et que le second ait 100 € de plus que le dernier.
Quelle somme doit il donner à chacun ?

Choix de l'inconnue:
Soit x la somme donnée au dernier (par exemple)
Mise en équation :
le dernier a x
le deuxième a x + 100
le troisième a ( x +100) + 200 = x + 300 ( il a 200 de plus que le second ).
la somme totale est 1600, donc
x + ( x +100 ) + ( x + 300 ) = 1600
Résolution de l'équation :
x + ( x +100 ) + ( x + 300 ) = 1600
3 x + 400 = 1600
3 x = 1600- 400
3 x = 1200
x = 1200 : 3
x = 400
Vérification : 400 + 500 + 700 = 1600

Conclusion : le dernier a 400 € , le deuxième 500 € et l'aîné 700 € .

B.

Un jardin a une forme rectangulaire. Il a vingt mètres de moins dans la largeur que dans la longueur. La longueur totale de la clôture qui l'entoure est 250 m.
Quelle est l'aire de ce jardin ?

Choix de l'inconnue:
pour calculer l'aire du jardin, il faut connaître sa longueur et sa largeur
Soit x la longueur du jardin en mètres.
Mise en équation :
la largeur est x - 20
le périmètre est la somme des longueur des côtés donc :
x + x -20 + x + x -20 = 4 x - 40
il vaut 250. Donc :
4 x - 40 = 250
Résolution de l'équation :
4 x - 40 = 250
4 x = 250 + 40
4 x =290
x = 290 : 4
x = 72,5
Vérification : 72,50 m est une longueur raisonnable pour un jardin.
La largeur est alors 72,5-20 = 52,5
Conclusion :
72,5 52,5 = 3806,25.
L'aire du jardin est 3806,25 m 2 .

C.

Un triangle a des côtés qui mesurent x + 4 cm, x cm et 9 cm.
Le côté de x + 4 est le côté le plus long.
Calculer x pour que ce triangle soit un triangle rectangle.

Le triangle est rectangle, donc d'après le théorème de Pythagore :

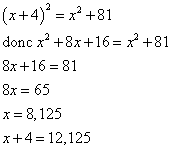
Les côtés du triangle mesurent 8,125 cm, 9 cm et 12,125 cm.

D.

Trouver cinq nombres entiers consécutifs dont la somme soit 1515.

Soit x le premier nombre.
les 5 nombres sont : x, x+1, x+2, x+3 et x+4
Leur somme est 1515, donc
x + x+1 + x+2 + x+3 + x+4 =1515
5x+10 = 1515
5x = 1505
x = 301
Les 5 nombres sont 301,302,303,304 et 305.

E.

À ce jour, l'âge du capitaine est le double de celui de Fred. Dans 5 ans, ils auront à eux deux 70 ans. Quel est l'âge du capitaine ?

Soit x l'âge de Fred.
L'âge du capitaine est 2x.
Dans 5 ans, Fred aura x+5 et le capitaine 2x+5.
Donc (x+5)+(2x+5)=70
3x+10 = 70
3x = 60
x = 20
Fred a 20 ans et le capitaine 40.

F.

Pour assister à un mach de foot, un groupe de 21 personnes a payé 90 € de plus qu'un groupe de 12 personnes.
Sachant que toutes les places sont au même prix, quel est le prix, en euros, d'une place ?

Dans le groupe de 21 personnes, il y a 9 personnes de plus que dans le groupe de 12 personnes. Ces 9 personnes ont payé 90 €.
Le prix d'une place est donc 10 €.

G.

Trouver le nombre entier x tel que la différence entre son quotient par et son produit par soit égal à 221.

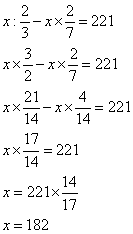
Le nombre est 182.

H.

Une personne à qui l'on demandait son âge a répondu :
« Si je vis jusqu'à 100 ans, il me reste encore à vivre les de l'âge que j'ai. » Quel est l'âge de cette personne ?

Soir x l'âge de cette personne.

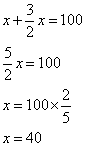
Cette personne a 40 ans.

I.

Une bouteille cylindrique de 12 cm de hauteur a une capacité de 1 L.
Quel est le rayon de sa base ? ( donner la valeur approchée au mm près ).

Soit r le rayon de la base. Le volume de la bouteille est
Le volume est 1L, donc1 dm3, donc 1000 cm3

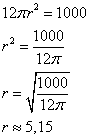
Le rayon de la bouteille est 5,2 cm environ.

J.

Une somme d'argent, placée à 6%, a rapporté les mêmes intérêts qu'une somme de 240 € placée à 5%. Calculer la somme inconnue.

Soit x la somme inconnue.
Les intérêts s'élèvent à 6%x, soit 0,06x.
240 € placés à 5% rapportent 0,05 240,c 'est à dire 12 €
0,06x =12, donc x = 12 : 0,06
x = 200.
La somme inconnue est 200 €.

K.

La somme de trois nombres pairs consécutifs est égale à 378.
Quels sont ces trois nombres ?

Le premier nombre pair est 2n, le deuxième 2n+2, le troisième 2n+4.
2n + 2n+2 + 2n+4 = 378
6n+6 = 378
6n = 372
n = 62
2n =124
Les trois nombres sont 124,126 et 128.

L.

Dans une classe de 3e , deux septièmes des élèves apprennent l'allemand, la moitié des élèves apprennent l'espagnol, et les six restants apprennent l'italien.
Combien y a t-il d'élèves dans cette classe ?

Soit x le nombre d'élèves dans cette classe.

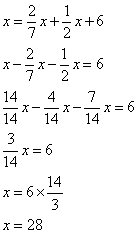
Il y a 28 élèves dans cette classe.