Volumes

Volumes
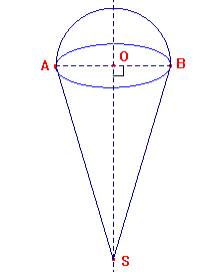
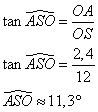
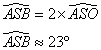
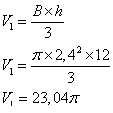
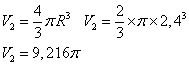
A. La glace contenue dans un cornet a la forme d'un cône surmonté d'une demi sphère. OS = 12 cm; OA = 2,4 cm. 1 ) Calculer la mesure de l'angle arrondie au degré. Dans AOS rectangle en O, Le triangle ASB e st isocèle en S, donc 2 ) Calculer le volume de la glace, arrondi au . Volume du cône : Volume de la demi boule: Volume total:
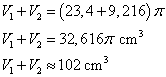
B. Le temple de la Concorde situé à Agrigente en Sicile possède 34 colonnes. On admet que : les colonnes sont toutes identiques et cylindriques chacune de ces colonnes a une hauteur h = 6,60 m et une base de rayon r = 0,70 m. le temple a la forme d'un parallélépipède rectangle de longueur L = 42,10 m, de largeur l = 19,70 m et de hauteur H = 9,80 m. Il contient les colonnes. 1. Calculer le volume d'une colonne, puis des 34 colonnes. Arrondir au près. 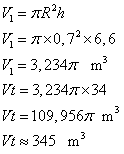2. Calculer le volume du temple. Arrondir au près. 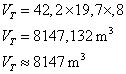3. Quel pourcentage du volume du temple représente le volume des colonnes ? Arrondir à l'unité. Les colonnes représentent environ 4% du volume du temple.
C. Une cuve de gaz propane est formée par un cylindre de 1,50 m de diamètre et de hauteur 3m complété à ses extrémités par deux demi sphères de diamètre 1,50 m. 1. Calculer la quantité de peinture nécessaire pour recouvrir cette cuve, sachant qu'un litre de peinture recouvre 8. La surface à peindre est la surface d'une sphère de rayon 0,75 m et de la face latérale d'un cylindre dont la hauteur est 3m et le rayon de la base 0,75m. La face latérale du cylindre est un rectangle dont les dimensions sont 3 m et la longueur d'un cercle de rayon 0,75 m, c'est à dire . Aire du rectangle : Aire de la sphère : Aire totale : L'aire totale de la cuve est environ 21,2 Il faut prévoir 3L de peinture ( qui recouvrent 24 ) 2. Calculer le volume de cette cuve. On ajoute le volume de la boule de rayon 0,75 m et le volume du cylindre. 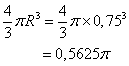Volume de la boule: Volume du cylindre : Volume total : La cuve contient environ 7 de gaz.
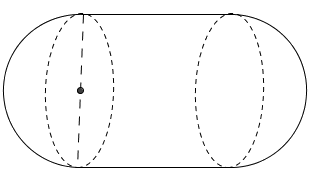
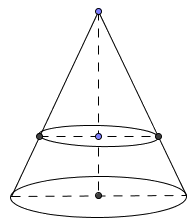
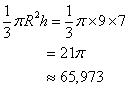
D. Un flacon de verre a la forme d'un cône de révolution. Sa hauteur est 7 cm. Sa base est un disque de 3 cm de rayon. Dans cet exercice, on ne tient pas compte de l'épaisseur du verre. 1. Calculer le volume de ce cône. On donnera la valeur exacte, puis la valeur arrondie au près. Volume du cône : Le volume du cône est d'environ 66 2. En réalité ce flacon est constitué par un réservoir et un bouchon obtenu en coupant le cône par un plan parallèle au plan de la base ( voir schéma ci-dessus ). La hauteur du bouchon est 4 cm. Calculer le volume du bouchon. On donnera la valeur exacte, puis la valeur arrondie au près. 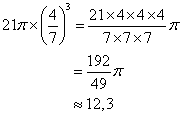Le bouchon est une réduction du cône de coefficient .On obtient son volume en multpliant le volume du cône par Volume du bouchon : Le volume du bouchon est d'environ 12 3. Le réservoir peut-il contenir 50 mL de parfum ? 66-12 = 54 Le volume du réservoir est environ 54 , c'est à dire 54 mL. ( 1 mL =1 ) Le flacon peut contenir 50 mL de parfum.
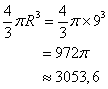
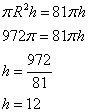
E. Une demi sphère de rayon 9 cm et un cylindre de même rayon ont le même volume. 1. Calculer le volume de la demi sphère . En donner la valeur arrondie au près. Le volume est environ 3054 2. Calculer la hauteur du cylindre. La hauteur du cylindre est 12 cm.
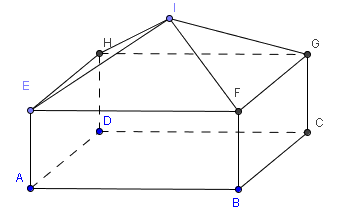
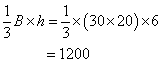
F. La maquette de maison représentée ci contre est composée - d'un pavé droit de dimensions : AB = 30 cm, BC = 20 cm et AE = 5 cm - surmontée d'une pyramide de hauteur 6 cm. 1. Calculer le volume V`1` de cette maquette. Volume du pavé droit : Volume de la pyramide : V`1` = 3000+1200 = 4200 Le volume total est 4200 . 2. Cette maquette est une réduction de coefficient 1/50 de la maison réelle. Déduire de la première question le volume V`2` ende la maison. La maison est un agrandissement de la maquette de coefficient 50, le volume est donc multiplié par . 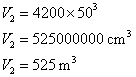3. Quelle est la hauteur totale réelle de la maison ? On obtient les longueurs réelles en multipliant les longueurs de la maquette par 50. La hauteur de la maison est 5,50 m.
retour