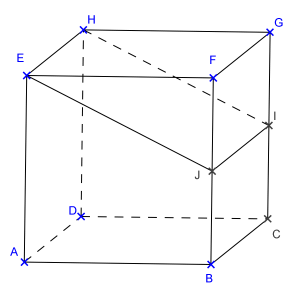
ABCDEFGH est un cube d'arête 10 cm.

1. a ) Calculer l'aire d'une face, puis l'aire totale du cube.
ABCDEFGH est un cube, donc ABFE est un carré.
AB AE = 100
L'aire d'une face est 100
Le cube a 6 faces, donc l'aire totale est 600 .

b ) Calculer le volume du cube.
.
Le volume de ce cube est 1000( 1 L).

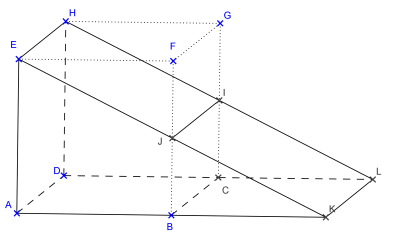
2. I est le milieu de [BF]
J est le milieu de [CG].

a ) Quelle est la nature de EJIH ?
EJIH est un rectangle.

b ) Calculer EJ.
ABFE est un carré, donc EFJ est rectangle en F.
Dans le triangle EJF rectangle en F, j'utilise le théorème de Pythagore

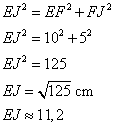
3. On découpe la partie du haut et on la fait basculer à droite.
a ) Montrer que E, J et K sont alignés.
et sont supplémentaires.
et sont symétriques par rapport à J, donc égaux.
Donc et sont supplémentaires et E,J et K sont alignés.

b ) On obtient un prisme droit à base triangulaire AKLDEH.
Comparer le volume du solide obtenu  et le volume du cube.
On a déplacé le prisme droit EJIHFG, donc les deux volumes sont égaux.

4. Calcul de l'aire du prisme droit .
a ) Quel est le nombre de faces du solide obtenu ?
Il a 5 faces, deux faces triangulaires superposables et trois faces rectangulaires.

b ) Calculer l'aire de AEK.
L'aire de AEK est égale à l'aire de ABFE, c'est à dire 100 .

c ) Calculer l'aire de EKLH
EKLH est un rectangle de longueur EK = 2EJ et de largeur EH.

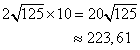
L'aire de EKLH est

d ) Calculer l'aire totale. Arrondir au .
La surface totale est formée de 5 carrés d'aire 100 et du rectangle EKLH.
L'aire totale est , c'est à dire environ 723,61 , donc
724 environ.

5. Comparer les deux aires.
Quel est le pourcentage d'augmentation ?

L'aire du prisme droit est supérieure à l'aire du cube. Il y a une augmentation de 124 environ.

Cela fait une augmentation de 21% environ.