Le poids et la masse dans le système solaire 
A. Sur une planète inconnue...
Un astronaute un peu perdu dans l'espace arrive sur une planète inconnue. Pour tenter de l'identifier, il fait une expérience : il rassemble plusieurs objets et mesure leur masse et leur poids.
Voici ses résultats :
| Masse m | 500 g |
2 kg |
8 kg |
5 kg |
1000 g |
7500 g |
0,01 t |
| Poids P | 4,3 N |
17,2 N |
68,8 N |
43 N |
8,6 N |
64,5 N |
86 N |
| Quotient P/m | 8,6 |
8,6 |
8,6 |
8,6 |
8,6 |
8,6 |
8,6 |
1. Tracer le graphique P = f ( m ) ( le poids en fonction de la masse )
On convertit toutes les masses en kg ( 1 t = 1000 kg )
2. Que remarque t-on ? Que peut on en déduire pour P et m ? Vérifier par le calcul en remplissant la dernière ligne du tableau.
Les points sont alignés sur une droite qui passe par l'origine du repère, donc il y a proportionnalité entre la masse et le poids.
En divisant le poinds ( en N) par la masse ( en g ) on obtient toujours 8,6. Le coefficient de proportionnalité est 8,6.
3. Répondre en utilisant le graphique :
si P = 20 N, alors m 
2,3 kg
si P = 60 N, alors m 7 kg
si m = 3,5 kg, alors P 30 N
4. Ecrire la fonction f qui à m associe P = f(m) ? Quelle est sa nature ?
f(m) = 8,6m. f est la fonction linéaire de coefficient 8,6.
5. Calculer l'image par f de 15. Quel est, sur cette planète, le poids d'une masse de 15 kg ?
f(15) = 8,6
15
Le poids d'une masse de 15 kg est 129 N.
6. Que vaut l'intensité de la pesanteur sur cette planète ?
Donner la relation entre P et m sur cette planète, en précisant les unités.
L'intensité de la pesanteur sur cette planète est 8,6.
P = 8,6 m, avec m en kilogrammes et P en Newtons.
7. L'astronaute retrouve le tableau suivant. Cela lui permet il de savoir sur quel objet céleste il se trouve ?
Mercure |
Vénus |
Terre |
Mars |
Jupiter |
Saturne |
Lune |
|
| Intensité de la pesanteur : g ( N/kg) | 3,78 |
8,6 |
9,8 |
3,72 |
22,9 |
9,05 |
1,6 |
L'astronaute est sur Vénus.
B. Les haltères...
1. Pour faire un peu d'exercice, l'astronaute a emmené 25 kg d'haltères.
Quel est le poids des haltères sur cette planète ?
f(25)= 8,6 25
= 215
Le poids des haltères est 215 N sur cette planète.
2. Sur Terre, ( gTterre = 9,8 N/kg )
a ) Quelle est la masse des haltères sur Terre ?
La masse des haltères est 25 kg sur Terre.
b ) Quel est leur poids sur Terre ?
259,8 = 217
Le poids des haltères est 217 N sur Terre.
3. D'après le tableau, sur quelle planète faut il être très musclé pour soulever ces haltères ? Calculer le poids de ces haltères sur cette planète.
Sur Jupiter, l'intensité de la peanteur est 22,8 N/kg
2522,8 = 570.
Le poids de haltères est 570 N sur Jupiter.
4. Quelle masse doit avoir un objet pour être aussi difficile à soulever sur Terre ?
570 : 9,8 58
La masse de l'objet doit être 58 kg
5. Sur quel objet céleste un enfant pourrait il facilement les soulever ? Justifier par un calcul.
251,6 = 40
Sur la Lune les haltères ont on poids de 40 N.
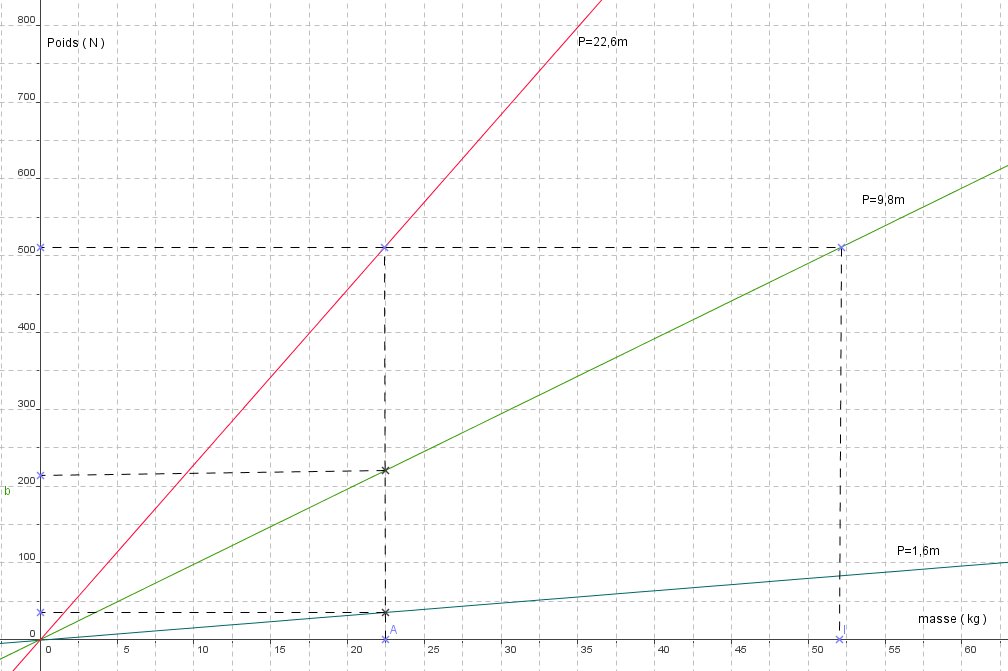
6. Sur chaque planète, le poids s'exprime par une fonction linéaire de la masse .
Ecrire cette fonction pour la Lune, la Terre et Mars. Représenter ces trois fonctions sur un même graphique.
Utiliser ce graphique pour retrouver les réponses aux questions précédentes.
Sur la Lune : f1(m) = 1,6m
Sur la Terre : f2 (m) = 9,8m
Sur Mars,: f3(m) = 22,8m
