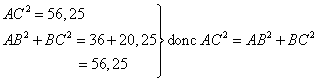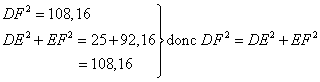Réciproque du théorème de Pythagore :

Si on connaît les longueurs des trois côtés d'un triangle, on peut prouver qu'il est rectangle.

Si, dans un triangle, le carré du côté le plus long est égal à la somme des carrés des deux autres côtés, alors ce triangle est un triangle rectangle.

Si BC² =AB² +AC² , alors ABC est rectangle en A.

Exemple :

ABC est tel que AB = 8 cm,
AC = 6 cm et BC = 10 cm.
ABC est il un triangle rectangle ?

Le côté le plus long est [BC].
BC² =100 ( ce sont des cm 2 )

AB² +AC² = 64 + 36 = 100

donc BC² =AB² +AC² , donc le triangle ABC est rectangle en A, d'après la réciproque du théorème de Pythagore.

Entraînement :

A.
ABC est un triangle tel que AB = 6 cm, BC = 4,5 cm et CA = 7,5 cm. ABC est il un triangle rectangle ?

Le côté le plus long est [AC].

donc ABC est un triangle rectangle en B, d'après la réciproque du théorème de Pythagore.

B.
DEF est un triangle tel que DE = 5 cm ; EF = 9,6 cm et DF = 10,4 cm.
DEF est il un triangle rectangle ?

Le côté le plus long est [DF].

donc DEF est un triangle rectangle en F, d'après la réciproque du théorème de Pythagore.