Semaine 7 : Théorème de Pythagore

2e

1e

Semaine 7 : Théorème de Pythagore

Théorème de Pythagore :

Le théorème de Pythagore permet de calculer la longueur d'un côté d'un triangle rectangle, connaissant les deux autres.

Dans un triangle rectangle, le carré de l'hypoténuse est égal à la somme des carrés des deux autres côtés.

Si ABC est un triangle rectangle en A, alors
BC² =AB² +AC²

Premier jour :

Calcul de la longueur de l'hypoténuse

Exemple :

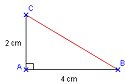
Calculer la valeur arrondie au mm de BC.

ABC est un triangle rectangle en A, donc j'utilise le théorème de Pythagore :

Entraînement :

A.

ABC est rectangle en B.
AB = 12 cm, BC = 5 cm.
Calculer AC.

B.

DEF est rectangle en E.
DE = 4 cm, EF = 7 cm.
Calculer la valeur arrondie au centième de DF.

Deuxième jour :

Calcul de la longueur d'un côté de l'angle droit

Exemple :

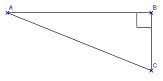
Calculer AC.

ABC est un triangle rectangle en A, donc j'utilise le théorème de Pythagore :

Entraînement :

A.

ABC est rectangle en B.
AB = 7 cm, AC = 9 cm.
Calculer la valeur arrondie au mm de BC.

B.

DEF est rectangle en E.
DE = 4 cm, DF = 8 cm.
Calculer la valeur arrondie au centième de EF.

Troisième jour :

Réciproque du théorème de Pythagore

Réciproque du théorème de Pythagore :

Si on connaît les longueurs des trois côtés d'un triangle, on peut prouver qu'il est rectangle.

Si, dans un triangle, le carré du côté le plus long est égal à la somme des carrés des deux autres côtés, alors ce triangle est un triangle rectangle.

Si BC² =AB² +AC² , alors ABC est rectangle en A.

Exemple :

ABC est tel que AB = 8 cm,
AC = 6 cm et BC = 10 cm.
ABC est il un triangle rectangle ?

Le côté le plus long est [BC].
BC² =100 ( ce sont des cm 2 )

AB² +AC² = 64 + 36 = 100

donc BC² =AB² +AC² , donc le triangle ABC est rectangle en A, d'après la réciproque du théorème de Pythagore.

Entraînement :

A.
ABC est un triangle tel que AB = 6 cm, BC = 4,5 cm et CA = 7,5 cm. ABC est il un triangle rectangle ?

B.
DEF est un triangle tel que DE = 5 cm ; EF = 9,6 cm et DF = 10,4 cm. DEF est il un triangle rectangle ?

Quatrième jour :

Dans l'espace.

Entraînement :

RS = 10 cm et le rayon du cercle de base est 2 cm.
Calculer la hauteur RH de ce cône de révolution, puis le volume du cône.

Cinquième jour :

Dans l'espace.

ABCDEFGH est un pavé droit de longueur AB = 7 cm, de largeur BD = 4 cm et de hauteur DH = 5 cm.
Calculer BC, puis BG.