1. AEG est un triangle rectangle.
Dans le triangle AEG, AE = 6 cm, AG = 8 cm et EG = 10 cm.
AE² + AG² = 6² + 8² = 36 + 64 = 100
EG² = 10² = 100.
Les deux quantités sont égales, la réciproque du théorème de Pythagore permet de conclure que le triangle AEG est un triangle rectangle en A.

2. Calcul des mesures des angles et .
Le triangle étant rectangle et connaissant les mesures des trois côtés on peut utiliser n'importe laquelle des notions cosinus, sinus ou tangente.
cos () =
cos () = = 0,6
La calculatrice donne : 2nd cos ( 6 : 10 ) = 53.13010235

53°.
Par complémentarité des angles aigus d'un triangle rectangle on a :
90 -53 = 37 donc 37°.

3. Calcul de AF.
[AF] étant une hauteur du triangle AEG, le triangleAFG est rectangle en F.
AF est le côté opposé à l'angle ou et [AG] est l'hypoténuse du triangle AFG.
On utilise le sinus de l'angle et on a :
sin() =

sin ( 37 ) =

AF = 8 sin ( 37 ) et donc AF 4,8 cm.

4. Calcul de GF et EF.
Dans le triangle rectangle AFG, on peut utiliser la notion de cosinus ou le théorème de Pythagore.
D'après le théorème de Pythagore on peut écrire :

FG² + FA² = AG²

ce qui donne 4,8² + FG² = 8² soit FG² = 8² - 4,8² = 40, 8 et donc
FG 6,4 cm.

F est un point du segment [EG] donc : EF + FG = EG ou encore EF = EG – FG , EF = 10 - 6,4
et par suite EF 3,6 cm.

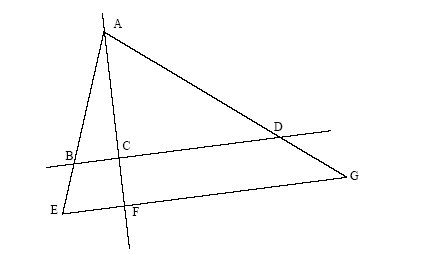
5. Calcul de AD.
Les point A, D et G sont alignés, les points A, B et E sont alignés et les droites (BD) et (EG) sont parallèles, on peut donc utiliser le théorème de Thalès et on peut écrire :
et donc
en utilisant la première égalité on a :

= 6.
AD = 6 cm.

6. Calcul de BD.
En utilisant l'égalité on a = 7,5
BD = 7,5 cm.

7. Calcul de AC.
Les point A, C et F sont alignés, les points A, B et E sont alignés et les droites (BC) et (EF) sont parallèles, on peut donc utiliser le théorème de Thalès et on peut donc écrire :
et donc et par suite
AC = et donc AC = 3,6 cm.

8. Calcul des aires des triangles ABD et AEG.
Aire de (ABD) = = = 13,5

Aire de (ABD) =13,5 cm².
Aire de (AEG) = = = 24

Aire de (AEG) = 24 cm².

9. Calcul de et remarque.
== 0,5625
= = 0,5625.

Le rapport des aires est égal au carré du rapport des longueurs.