Théorème de Pythagore

Théorème de Pythagore :

On nomme a, b et c les longueurs des trois côtés d'un triangle.
Les triangles pour lesquels on a la relation a²+ b² = c² sont tous les triangles rectangles dont l'hypoténuse est le côté de longueur c, et seulement eux.

Dans un triangle rectangle, le carré de l'hypoténuse est égal à la somme des carrés des deux autres côtés.

Si ABC est un triangle rectangle en A, alors BC² =AB² + AC² .

démonstration

Si, dans un triangle, le carré du côté le plus long est égal à la somme des carrés des deux autres côtés, alors ce triangle est un triangle rectangle.

Si BC² =AB² +AC² , alors ABC est rectangle en A.

D'après le théorème de Pythagore :

Si, dans un triangle, le carré du côté le plus long n'est pas égal à la somme des carrés des deux autres côtés, alors ce triangle n'est pas un triangle rectangle.

Si BC est le côté le pluslong et BC² AB² +AC² , alors ABC n'est pas un triangle rectangle.

Théorème de Pythagore
Théorème de Pythagore : On nomme a, b et c les longueurs des trois côtés d'un triangle. Les triangles pour lesquels on a la relation a²+ b² = c² sont tous les triangles rectangles dont l'hypoténuse est le côté de longueur c, et seulement eux.
Utilisation du théorème de Pythagore pour calculer la longueur d'un côté d'un triangle rectangle :
Dans un triangle rectangle, le carré de l'hypoténuse est égal à la somme des carrés des deux autres côtés. Si ABC est un triangle rectangle en A, alors BC² =AB² + AC² . démonstration	Le théorème de Pythagore sert à calculer des longueurs dans un triangle rectangle
Calcul de la longueur de l'hypoténuse : Calculer BC. En donner la valeur arrondie au mm. ABC est un triangle rectangle en A, donc j'utilise le théorème de Pythagore : Remarque : est, par définition, le nombre dont le carré est égal à 34. La calculatrice en donne une valeur approchée. La valeur exacte de BC est cm	Calcul de la longueur d'un côté de l'angle droit : Calculer AC. En donner la valeur arrondie au mm. ABC est un triangle rectangle en A, donc j'utilise le théorème de Pythagore :
Utilisation du théorème de Pythagore pour prouver qu'un triangle est rectangle :
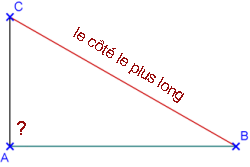
Si, dans un triangle, le carré du côté le plus long est égal à la somme des carrés des deux autres côtés, alors ce triangle est un triangle rectangle. Si BC² =AB² +AC² , alors ABC est rectangle en A.	Si on connaît les longueurs des trois côtés d'un triangle, on peut prouver qu'il est rectangle.
Comment prouver qu'un triangle est un triangle rectangle : ABC est tel que AB = 8 cm, AC = 6 cm et BC = 10 cm. ABC est il un triangle rectangle ? Le côté le plus long est [BC]. BC² =100 ( ce sont des cm² ) AB² +AC² = 64 + 36 = 100 donc BC² =AB² +AC², donc le triangle ABC est rectangle en A, d'après le théorème de Pythagore. Il faut comparer les valeurs exactes de ces deux nombres. On ne peut pas prouver une égalité en utilisant des valeurs approchées !
Utilisation du théorème de Pythagore pour prouver qu'un triangle n'est pas rectangle :
D'après le théorème de Pythagore : Si, dans un triangle, le carré du côté le plus long n'est pas égal à la somme des carrés des deux autres côtés, alors ce triangle n'est pas un triangle rectangle. Si BC est le côté le pluslong et BC² AB² +AC² , alors ABC n'est pas un triangle rectangle.	Si on connaît les longueurs des trois côtés d'un triangle, on peut prouver qu'il n'est pas rectangle.
Comment prouver qu'un triangle n'est pas un triangle rectangle : ABC est tel que AB = 9 cm, AC = 7 cm et BC = 6 cm. ABC est il un triangle rectangle ? Le côté le plus long est [AB]. AB² = 81 ( ce sont des ) AC² +BC² = 49 + 36 = 85 AB ² AC² +BC², donc le triangle ABC n'est pas un triangle rectangle, d'après le théorème de Pythagore.