Des constructions géométriques de segments dont la longueur est cm.

(le but n'est pas de construire un segment de longueur approximative , c'est à dire environ 3,9 cm, mais de trouver des constructions "exactes" de tels segments).

Première méthode :
Le point H est tel que AH = 1 et AB = a.
Montrer que AD =

D est un point du cercle de diamètre [AB], donc ADB est rectangle en D.
Dans le triangle ADB rectangle en D,

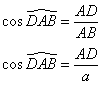
Dans le triangle ADH rectangle en H,

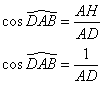
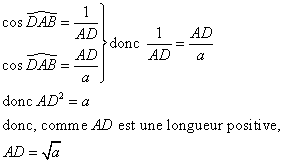
Utiliser cette méthode pour tracer un segment de longueur cm. Expliquer.
Tracer un cercle de diamètre15 cm. Placer un point H sur le diamètre à 1 cm de A et tracer la perpendiculaire à [AB] passant par H. Le point d'intersection de cette droite et du cercle est le point D tel que AD = cm.

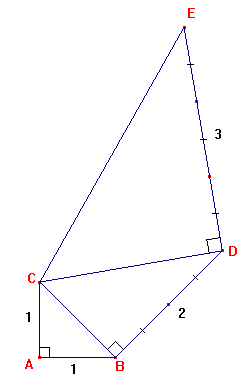
Deuxième Méthode : "escargot de Pythagore"

ABC, BCD et CDE sont trois triangles rectangles.
AC = 1 cm ; BD = 2 cm et DE = 3 cm.
Montrer que CE = cm.

ABC est un triangle rectangle en A, donc j'utilise le théorème de Pythagore :

CBD est un triangle rectangle en B, donc j'utilise le théorème de Pythagore :

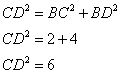
CDE est un triangle rectangle enD, donc j'utilise le théorème de Pythagore :

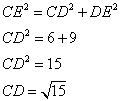
Le mathématicien Louis Lagrange a démontré que l'on peut tracer des segments de longueur , pour tout nombre entier a, en utilisant cette méthode avec trois triangles rectangles.
Appliquer cette méthode à la construction d'un segment de longueur cm.
Essayer avec AB = 1, BD = 1 et DE = 4 .

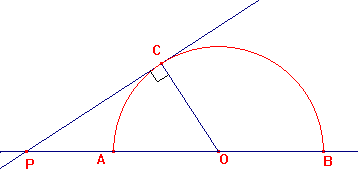
Troisième méthode :
(PC) est tangente en C au cercle de diamètre [AB] et de centre O.
On pose PO = x et AO = r
Calculer et en fonction de x et r. Que remarque t-on ?

(PC) est tangente en C au cercle de centre O, donc (PC) (CO).
Dans le triangle POC rectangle en C, j'utilise le théorème de Pythagore:

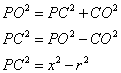
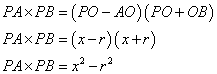
donc

En déduire la construction d'un segment de longueur cm.
Pour PA = 3 cm et PB = 5 cm, on obtient .
Il faut donc construire un cercle de rayon 1 cm et placer P à 3 cm de A.