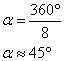A.

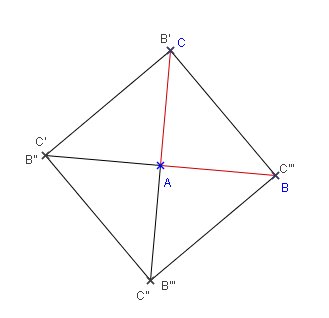
ABC est un triangle rectangle et isocèle en A.
Quel polygone obtient-on en traçant l'image du triangle ABC dans la rotation de sommet A, de sens direct et d'angle 90°, puis en recommençant ?

Les diagonales de BCC'C'' sont perpendiculaires, se coupent en leur milieu et ont la même longueur. Donc BCC'C'' est un carré.

B.

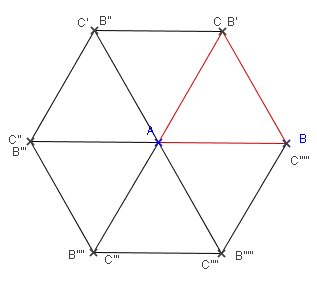
ABC est un triangle équilatéral.
Quel polygone obtient-on en traçant l'image du triangle ABC dans la rotation de centre A de sens direct et d'angle 60°, puis en recommençant ?

On obtient un polygone régulier à 6 côtés : un hexagone régulier.

C.

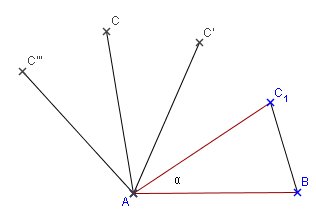
ABC est un triangle isocèle en A
On utilise une rotation de centre A et de sens direct et d'angle .
Quelle doit être la mesure de A pour que l'on obtienne un triangle équilatéral ? Un pentagone régulier ? Un heptagone régulier ? Un octogone régulier ? Un polygone régulier à n côtés ?

Pour obtenir un polygone régulier à n côtés, il faut partager l'angle au centre en n angles égaux.
Donc
Dans le cas d'un triangle équilatéral :

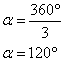
Dans le cas d'un pentagone régulier ( 5 côté ) :

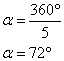
Dans le cas d'un heptagone régulier ( 7 côtés ) :

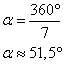
Dans le cas d'un octogone régulier ( 8 côtés ) :