A. ABC est un triangle tel que AB = 6,9 cm, BC = 9,2 cm et AC = 11,5 cm.
1. Montrer que ABC est un triangle rectangle.
2. a) Calculer la valeur arrondie au degré de .
b) En déduire la valeur arrondie au degré de
3. Soit D le symétrique de B par rapport à (AC). Calculer l'aire du quadrilatère ABCD.

B. Tracer un cercle de centre O et de rayon 5 cm. Soit [AB] un diamètre de ce cercle.
Soit M le point de [OA] tel que OM = 1,7 cm.
La perpendiculaire à (AB) passant par M coupe le cercle en C et D.
1. a ) Quelle est la longueur de [OC] ?
b ) Calculer la valeur arrondie au degré de .
c ) En déduire la valeur arrondie au degré de .
2. Montrer que la valeur arrondie au degré de est 35°.
3. Montrer que la valeur arrondie au millimètre de BC est 8,2 cm.
4. Que peut on dire du triangle ABC ? Le démontrer.
5. Calculer la valeur arrondie au millimètre de AC.

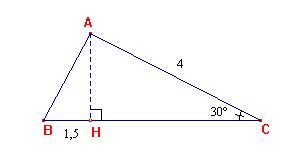
C. Un élément de charpente a la forme ci-contre.
Calculer la longueur de la poutre CD, arrondie au cm, sachant que AB = 7,20 m et que la pente du toit doit être de 32°.

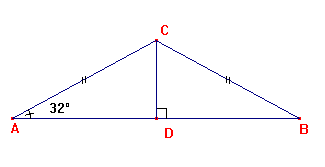
D. ABC est un triangle rectangle en A tel que AC = 5 cm et BC = 13 cm.
1. Calculer AB.
2. Monter que la valeur arrondie au degré de la mesure de est 23°.
3. Tracer le cercle circonscrit à ABC. Soit O son centre. Préciser la position du point O.
4. Quelle est la valeur arrondie au degré de la mesure de ? Justifier.
5. Le cercle de centre A qui passe par C coupe le cercle circonscrit à ABC au point E. Quelle est la valeur arrondie au degré de la mesure de ? Justifier.

E. Soit C un cercle de centre O et de rayon 6 cm. Soit [AB] un diamètre de ce cercle.
Soit M un point de C tel que = 36°.
1. Montrer que ABM est un triangle rectangle.
2. Calculer AM. Donner sa valeur arrondie au millimètre près.
3. Construire la droite d, tangente en B au cercle C . Soit P le point de d tel que AP = 14 cm.
Montrer que ABP est un triangle rectangle.
4. Calculer PB. En donner la valeur arrondie au centième.

1. Calculer AH.

2. En déduire la valeur arrondie à un degré près de la mesure de l'angle .

3. ABC est-il un triangle rectangle ?