A. ABC est un triangle tel que AB = 6,9 cm, BC = 9,2 cm et
AC = 11,5 cm.
1. Montrer que ABC est un triangle rectangle.

Le côté le plus long est AC.

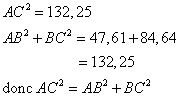
Donc le triangle ABC est rectangle en B d'après la réciproque du théorème de Pythagore.
2. a) Calculer la valeur arrondie au degré de .
Dans le triangle ACB rectangle en B,

b) En déduire la valeur arrondie au degré de

Les deux angles aigus d'un triangle rectangle sont coimplémentaires, donc

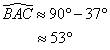
3. Soit D le symétrique de B par rapport à (AC).
Calculer l'aire du quadrilatère ABCD.

ADC est le symétrique de ABC par rapport à (AC) et la symétrie axiale conserve les aires, donc

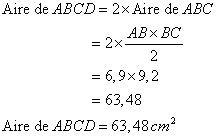
B. Tracer un cercle de centre O et de rayon 5 cm. Soit [AB] un diamètre de ce cercle.
Soit M le point de [OA] tel que OM = 1,7 cm.
La perpendiculaire à (AB) passant par M coupe le cercle en C et D.

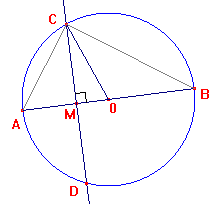
1. a ) Quelle est la longueur de [OC] ?

[OC]est un rayon du cercle, donc OC = 5 cm.
b ) Calculer la valeur arrondie au degré de .

Dans le triangle OCM rectangle en M,

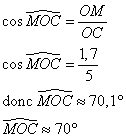
c ) En déduire la valeur arrondie au degré de .

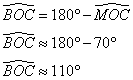
2. Montrer que la valeur arrondie au degré de est 35°

[OB] et [OC] sont deux rayons du cercle, donc OBC est isocèle en O. Donc

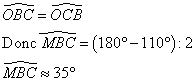
3. Montrer que la valeur arrondie au millimètre de BC est 8,2 cm.

Dans le triangle MBC rectangle en M,

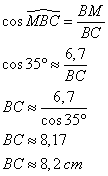
4. Que peut on dire du triangle ABC ? Le démontrer.

C est un point du cercle de diamètre [AB], donc ABC est rectangle en C.

5. Calculer la valeur arrondie au millimètre de AC.

Dans le triangle ABC rectangle en C

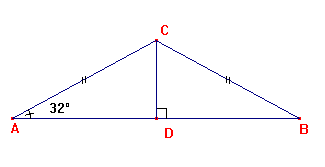
C. Un élément de charpente a la forme ci-contre. Calculer la longueur de la poutre CD, arrondie au cm, sachant que AB = 7,20 m et que la pente du toit doit être de 32°.

ABC est un triangle isocèle, donc la hauteur [CD] est aussi la médiane, donc D est le milieu de [AB].
AD = 3,60 m.
Dans le triangle ACD rectangle en D,

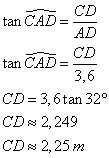
D. ABC est un triangle rectangle en A tel que AC = 5 cm et BC = 13 cm

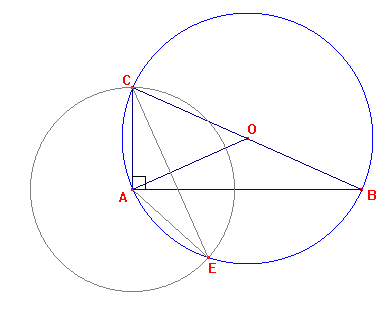
1. Calculer AB.

ABC est un triangle rectangle en A, donc j'utilise le théorème de Pythagore.

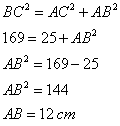
2. Monter que la valeur arrondie au degré de la mesure de est 23°.

Dans ABC rectangle en A,


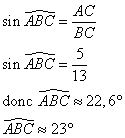
3. Tracer le cercle circonscrit à ABC. Soit O son centre. Préciser la position du point O.
Le cercle circonscrit à un triangle rectangle a pour centre le milieu de l'hypoténuse, donc O est le milieu de [BC].
4. Quelle est la valeur arrondie au degré de la mesure de ? Justifier.
est l'angle au centre qui intercepte le même arc que , donc
mesure le double de , c'est à dire environ 46°.

5. Le cercle de centre A qui passe par C coupe le cercle circonscrit à ABC au point E. Quelle est la valeur arrondie au degré de la mesure de ? Justifier.

est un angle inscrit qui intercepte le même arc que , donc et sont égaux. Donc mesure envoron 23°.

E. Soit C un cercle de centre O et de rayon 6 cm. Soit [AB] un diamètre de ce cercle.
Soit M un point de C tel que = 36°.

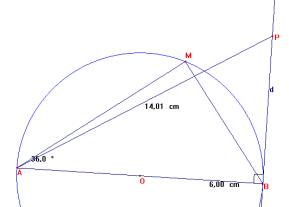
1. Montrer que ABM est un triangle rectangle.

M est un point du cercle de diamètre [AB], donc ABM est rectangle en M.

2. Calculer AM. Donner sa valeur arrondie au millimètre près.

Dans AMB rectangle en M,

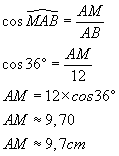
3. Construire la droite d, tangente en B au cercle C . Soit P le point de d tel que AP = 14 cm. Montrer que ABP est un triangle rectangle.

Une tangente à un cercle est perpendiculaire au rayon. Donc ABP est rectangle en P.

4. Calculer PB. En donner la valeur arrondie au centième.

ABP est rectangle en P, donc, d'après le théorème de Pythagore,

Dans le triangle ABC de hauteur [AH] représenté ci contre, on donne
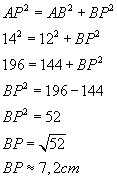
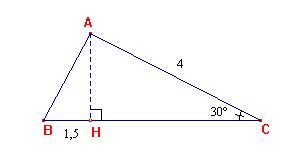
AC = 4 cm, BH = 1,5 cm et .
1. Calculer AH.

AHC est un triangle rectangle en H.

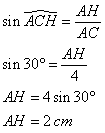
2. En déduire la valeur arrondie à un degré près de la mesure de l'angle .
Dans le triangle BAH rectangle en H,

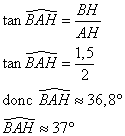
3. ABC est-il un triangle rectangle ?
Les angles aigues d'untriangle rectangle sont complémentaires, donc
37+60>90, donc ABC n'est pas un triangle rectangle.